VALOR ABSOLUTO
El valor absoluto de un número es, el mismo número si el número es positivo o cero, y el opuesto si el número es negativo.
Se
suele decir que el valor absoluto de un número es el número sin tener
en cuenta su signo. Por ejemplo: abs (5) = |5| = 5, abs ( 3´4) = |3´4| =
3´4 abs (-2 ) = | -2| = 2, abs ( 0) = |0| = 0, abs ( -34´7) = | -34´7| =
34´7
Sirve por ejemplo para calcular la distancia entre dos puntos: La distancia entre los puntos x = 5 y x = 7 es d = | 7 - 5| = 2
Claramente la distancia entre x = 7 y x = 5 es la misma por lo que d = | 5 - 7| = | -2| = 2
El
valor absoluto está relacionado con las nociones de magnitud, distancia
y norma en diferentes contextos matemáticos y físicos. El concepto de
valor absoluto de un número real puede generalizarse a muchos otros
objetos matemáticos, como son los cuaterniones, anillos ordenados,
cuerpos o espacios vectoriales.
¿COMO SE RESUELVE EL VALOR ABSOLUTO?
Vamos a empezar primero por la definición de valor absoluto.
El valor absoluto es una función el cual siempre devuelve un valor positivo. El valor absoluto se denota así:
f(x) = |x|
Y los posibles resultados son:
f(a) = |a| = a
f(-a) = |-a| = -(-a) = a
Lo
anterior significa que si el argumento de la función valor absoluto es
positivo, entonces la función devuelve su argumento sin tocarlo, si
embargo, si el argumento es negativo entonces multiplica el valor del
argumento por -1 y se vuelve positivo.
Un ejemplo numérico:
f(5) = |5| = 5
f(-5) = |-5| = -(-5) = 5
Fácil, verdad?
Ahora
vamos a complicarlo un poco más, que pasaría si el argumento fuese una
función en vez de un valor constante? es decir, que pasaría si se tiene
lo siguiente?:
|2x - 1| =???
Pues habría dos posibles soluciones, partiendo de la definición de valor absoluto tendríamos:
|2x - 1| = 2x - 1 si x > 0
|2x - 1| = -(2x - 1) = 1 - 2x si x < 0
Y listo, problema resuelto. Pero el valor absoluto también se presente con desigualdades:
|x - 7| < 4
Como crees que se podría resolver esta desigualdad?
Pues de nuevo, partimos de la de f. de valor absoluto:
|x - 7| < 4 ==> x - 7 < 4 si x > 0
|x - 7| < 4 ==> -(x - 7) < 4 ==> 7 - x > -4 si x < 0
Fíjate
lo que paso en la última desigualdad. Cambió el signo. Por qué? pues
por que multiplicamos por -1 y cuando hacemos esto el signo de la
desigualdad se invierte. Es decir si tenemos algo así:
x < 7 y multiplicamos por -1 quedaría:
-x > -7
Formalmente, el valor absoluto o módulo de todo número real 
está definido por:2
siempre será mayor o igual que cero y nunca negativo.
Desde un punto de vista geométrico, el valor absoluto de un número real es siempre positivo o cero,
pero nunca negativo. En general, el valor absoluto de la diferencia de
dos números reales es la distancia entre ellos. De hecho, el concepto de
función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
La función valor absoluto una función continua definida por trozos.
está definido por:2
siempre será mayor o igual que cero y nunca negativo.Desde un punto de vista geométrico, el valor absoluto de un número real
es siempre positivo o cero,
pero nunca negativo. En general, el valor absoluto de la diferencia de
dos números reales es la distancia entre ellos. De hecho, el concepto de
función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.La función valor absoluto una función continua definida por trozos.
Propiedades fundamentales
 |
No negatividad |
 |
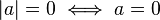Definición positiva |
 |
Propiedad multiplicativa |
 |
Desigualdad triangular (Véase también Propiedad aditiva) |
No hay comentarios:
Publicar un comentario