domingo, 2 de febrero de 2014

MATRICES

MATRICES

Para otros usos de este término, véase Matriz. En matemáticas, una matriz es un arreglo bidimensional de números, y en su mayor generalidad de elementos de un anillo. Las matrices se usan generalmente para describir sistemas de ecuaciones lineales, sistemas de ecuaciones diferenciales o representar una aplicación lineal (dada una base). Las matrices se describen en el campo de la teoría de matrices.
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar las aplicaciones lineales; en este último caso las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.


Ejemplo

Dada la matriz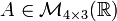 A\in\mathcal{M}_{4\times 3}(\mathbb{R})
A = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ 6 & 0 & 5 \end{bmatrix}
es una matriz de tamaño 4\times 3. La entrada a_{23}\,\! es 7.
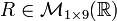
La matriz R\in\mathcal{M}_{1\times 9}(\mathbb{R})
R = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \end{bmatrix}
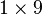es una matriz de tamaño 1\times 9: un vector fila con 9 entradas.

Suma o adición

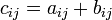Sean A,B\in\mathcal{M}_{n\times m}(\mathbb{K}). Se define la operación de suma o adición de matrices como una operación binaria +:\mathcal{M}_{n\times m}(\mathbb{K})\times\mathcal{M}_{n\times m}(\mathbb{K})\longrightarrow\mathcal{M}_{n\times m}(\mathbb{K}) tal que (A,B)\mapsto C=A+B y donde c_{ij}=a_{ij}+b_{ij}\,\! en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo \mathbb{K}. Por ejemplo, la entrada c_{12}\,\! es igual a la suma de los elementos a_{12}\,\! y b_{12}\,\! lo cual es a_{12}+b_{12}\,\!.
Veamos un ejemplo más explícito. Sea A,B\in\mathcal{M}_{3}(\mathbb{R})
\begin{bmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{bmatrix} + \begin{bmatrix} 1 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1+1 & 3+0 & 2+5 \\ 1+7 & 0+5 & 0+0 \\ 1+2 & 2+1 & 2+1 \end{bmatrix} = \begin{bmatrix} 2 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \end{bmatrix}
No es necesario que las matrices sean cuadradas:































\begin{bmatrix} 2 & 2 & 1 \\ 3 & 2 & 1 \\ 2 & 3 & 2 \\ 2 & 0 & 4 \end{bmatrix} \quad + \quad \begin{bmatrix} 0 & 1 & 4 \\ 1 & 4 & 0 \\ 2 & 1 & 1 \\ 0 & 2 & 2 \end{bmatrix} \quad = \quad \begin{bmatrix} 2 & 3 & 5 \\ 4 & 6 & 1 \\ 4 & 4 & 3 \\ 2 & 2 & 6 \end{bmatrix}
 IGUALDAD DE MATRICES
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales

Para que las matrices  A  y  B  sean iguales, se tiene que cumplir que  a = 7  y  b = 5.

TIPOS DE MATRICES

  • Matriz Fila
  • Matriz Columna
  • Matriz Rectangular
  • Matriz Transpuesta
  • Matriz Nula
  • Matriz Cuadrada

CLASES DE MATRICES CUADRADAS

  1. Matriz triangular superior
  2. Matriz triangular inferior
  3. Matriz diagonal
  4. Matriz escalar
  5. Matriz identidad o unidad
  6. Matriz regular
  7. Matriz singular
  8. Matriz idempotente
  9. Matriz involutiva
  10. Matriz simétrica
  11. Matriz antisimetrica o hemisimetrica
  12. Matriz ortogonal

Publicado por en

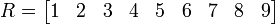
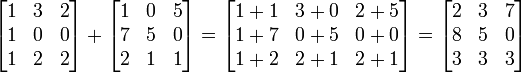
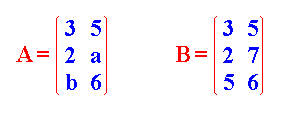
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)