domingo, 2 de febrero de 2014

LA REGLA DE SARRUS

LA REGLA DE SARRUS 

 

La regla de Sarrus es un método fácil para memorizar y calcular el determinante de una matriz 3×3. Recibe su nombre del matemático francés Pierre Frédéric Sarrus..

Considérese la matriz 3×3:
M = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}
Su determinante se puede calcular de la siguiente manera:
En primer lugar, repetir las dos primeras columnas de la matriz a la derecha de la misma de manera que queden cinco columnas en fila. Después sumar los productos de las diagonales descendentes (en línea continua) y sustraer los productos de las diagonales ascendentes (en trazos). Esto resulta en:
\det \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} =
= a_{11} a_{22} a_{33} + \; a_{12} a_{23} a_{31} + \; a_{13} a_{21} a_{32} - \; a_{31} a_{22} a_{13} - \; a_{32} a_{23} a_{11} - \; a_{33} a_{21} a_{12}
Un proceso similar basado en diagonales también funciona con matrices 2×2:
\det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a_{21}a_{12}
Esta regla mnemotécnica es un caso especial de la fórmula de Leibniz y ha sido conocido que no puede aplicar para matrices mayores a 3×3. Sin embargo, en octubre del año 2000, el matemático Gustavo Villalobos Hernández de la Universidad de Guadalajara, en México, encontró un método para calcular el determinante de una matriz de 4×4, sin reducir a determinantes de 3×3 con la matriz adjunta y el menor complementario. Su resultado es una extensión completa de la Regla de Sarrus, ya que utiliza el mismo método, obteniendo directamente los 24 términos requeridos para su cálculo.

Método de Sarrus

El método de Sarrus es una utilidad para calcular determinantes de orden 3.
Los términos con signo + están formados por los elementos de la diagonal principal y los de las diagonales paralelas con su correspondiente vértice opuesto.
positivo

Los términos con signo - están formados por los elementos de la diagonal secundaria y los de las diagonales pelaarals con su correspondiente vértice opuesto.
negativo

Ejemplo

sarrus
Publicado por en

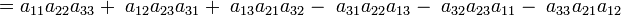
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)