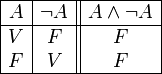ESTADÍSTICA
La estadística es comúnmente considerada
como una colección de hechos numéricos expresados en términos de una
relación sumisa, y que han sido recopilados a partir de otros datos
numéricos.
Kendall y Buckland (citados por Gini V.
Glas / Julian C. Stanley, 1980) definen la estadística como un valor
resumido, calculado, como base en una muestra de observaciones que
generalmente, aunque no por necesidad, se considera como una estimación
de parámetro de determinada población; es decir, una funcion de bvalores
de muestra.
"La estadística es una técnica especial
apta para el estudio cuantitativo de los fenómenos de masa o colectivo,
cuya mediación requiere una masa de observaciones de otros fenómenos más
simples llamados individuales o particulares". (Gini, 1953.
Murria R. Spiegel, (1991) dice: "La
estadística estudia los métodos científicos para recoger, organizar,
resumir y analizar datos, así como para sacar conclusiones válidas y
tomar decisiones razonables basadas en tal análisis.
"La estadística es la ciencia que trata de
la recolección, clasificación y presentación de los hechos sujetos a
una apreciación numérica como base a la explicación, descripcion y
comparación de los fenómenos". (Yale y Kendal, 1954).
Cualquiera sea el punto de vista, lo
fundamental es la importancia científica que tiene la estadística,
debido al gran campo de aplicación que posee. Otros autores tienen
definiciones de la Estadística semejantes a las anteriores, y algunos
otros no tan semejantes. Para Chacón esta se define como "la ciencia que
tiene por objeto el estudio cuantitativo de los colectivos"; otros la
definen como la expresión cuantitativa del conocimiento dispuesta en
forma adecuada para el escrutinio y análisis. La más aceptada, sin
embargo, es la de Minguez, que define la Estadística como "La ciencia
que tiene por objeto aplicar las leyes de la cantidad a los hechos
sociales para medir su intensidad, deducir las leyes que los rigen y
hacer su predicción próxima".
Utilidad e importancia
Los métodos estadísticos tradicionalmente
se utilizan para propósitos descriptivos, para organizar y resumir datos
numéricos. La estadística discriptiva, por ejemplo trata de la
tabulacion de datos, su presentación en forma gráfica o ilustrativa y
el calculo de medidas descriptivas.
División de la Estadística
La Estadística para su mejor estudio se ha
dividido en dos grandes ramas: la Estadística Descriptiva, la
Inferencial e Inductiva.
Estadística Descriptiva
Tienen por objeto fundamental describir y
analizar las características de un conjunto de datos, obteniéndose de
esa manera conclusiones sobre las características de dicho conjunto y
sobre las relaciones existentes con otras poblaciones, a fin de
compararlas. No obstante puede no solo referirse a la observación de
todos los elementos de una población (observación exhaustiva) sino
también a la descripción de los elementos de una muestra (observación
parcial).
En relación a la estadística descriptiva,
Ernesto Rivas González dice; "Para el estudio de estas muestras, la
estadística descriptiva nos provee de todos sus medidas; medidas que
cuando quieran ser aplicadas al universo total, no tendrán la misma
exactitud que tienen para la muestra, es decir al estimarse para el
universo vendrá dada con cierto margen de error; esto significa que el
valor de la medida calculada para la muestra, en el oscilará dentro de
cierto límite de confianza, que casi siempre es de un 95 a 99% de los
casos.
Estadística Inferencial
Se deriva de muestras, de observaciones
hechas sólo acerca de una parte de un conjunto numeroso de elementos y
esto implica que su análisis requiere de generalizaciones que van más
allá de los datos. Como consecuencia, la característica más importante
del reciente crecimiento de la estadística ha sido un cambio en el
énfasis de los métodos que describen a métodos que sirven para hacer
generalizaciones. La Estadística Inferencial investiga o analiza una
población partiendo de una muestra tomada. Según Berenson y Levine;
Estadística Inferencial son procedimientos estadísticos que sirven para
deducir o inferir algo acerca de un conjunto de datos numéricos
(población), seleccionando un grupo menor de ellos (muestra). El
objetivo de la inferencia en investigacion cientifica y tecnológica
radica en conocer clases numerosas de objetos, personas o eventos a
partir de otras relativamente pequeñas compuestas por los mismos
elementos.
En relación a la estadística descriptiva y
la inferencial, Levin & Rubin (1996) citan los siguientes ejemplos
para ayudar a entender la diferencia entre las dos.
Método Estadístico
El conjunto de los métodos que se utilizan
para medir las características de la informacion, para resumir los
valores individuales, y para analizar los datos a fin de extraerles el
máximo de información, es lo que se llama métodos estadísticos. Los
métodos de análisis para la información cuantitativa se pueden dividir
en los siguientes seis pasos:
Población: El concepto de población en
estadística va más allá de lo que comúnmente se conoce como tal. Una
población se precisa como un conjunto finito o infinito de personas u
objetos que presentan características comunes.
"Una población es un conjunto de todos los
elementos que estamos estudiando, acerca de los cuales intentamos sacar
conclusiones". Levin & Rubin (1996).
"Una población es un conjunto de elementos que presentan una característica común". Cadenas (1974).
Muestra: "Se llama muestra a una parte de la población a estudiar que sirve para representarla". Murria R. Spiegel (1991).
"Una muestra es una colección de algunos elementos de la población, pero no de todos". Levin & Rubin (1996).
"Una muestra debe ser definida en base de
la población determinada, y las conclusiones que se obtengan de dicha
muestra solo podrán referirse a la población en referencia", Cadenas
(1974).
Muestreo: Esto no es más que el
procedimiento empleado para obtener una o más muestras de una población;
el nuestreo es una técnica que sirve para obtener una o más muestras de
población.
Tipos de muestreo
Existen dos métodos para seleccionar
muestras de poblaciones; el muestreo no aleatorio o de juicio y el
muestreo aleatorio o de probabilidad En este último todos los elementos
de la población tienen la oportunidad de ser escogidos en la muestra.
Una muestra seleccionada por muestreo de
juicio se basa en la experiencia de alguien con la población. Algunas
veces una muestra de juicio se usa como guía o muestra tentativa para
decidir como tomar una muestra aleatoria más adelante. Las muestras de
juicio evitan el análisis estadístico necesario para hacer muestras de
probabilidad.
Datos estadísticos
Los datos estadísticos no son otra cosa
que el producto de las observaciones efectuadas en las personas y
objetos en los cuales se produce el fenómeno que queremos estudiar.
Dicho en otras palabras, son los antecedentes (en cifras) necesarios
para llegar al conocimiento de un hecho o para reducir las consecuencias
de este.
Los datos estadísticos se pueden encontrar
de forma no ordenada, por lo que es muy difícil en general, obtener
conclusiones de los datos presentados de esta manera. Para poder obtener
una precisa y rápida información con propósitos de descripción o
análisis, estos deben organizarse de una manera sistemática; es decir,
se requiere que los datos sean clasificados. Esta clasificación u
organizacion puede muy bien hacerse antes de la recopilación
Clasificación de los datos
Los datos estadísticos pueden ser clasificados en cualitativos, cuantitativos, cronológicos y geográficos.
Datos Cualitativos:
cuando los datos son cuantitativos, la diferencia entre ellos es de clase y no de cantidad.
Datos cuantitativos:
cuando los valores de los datos representan diferentes magnitudes, decimos que son datos cuantitativos.
Datos cronológicos:
cuando los valores de los datos varían en
diferentes instantes o períodos de tiempo, los datos son reconocidos
como cronológicos.



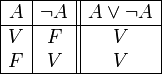
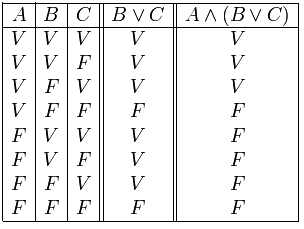
 está definido por:
está definido por:

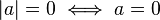





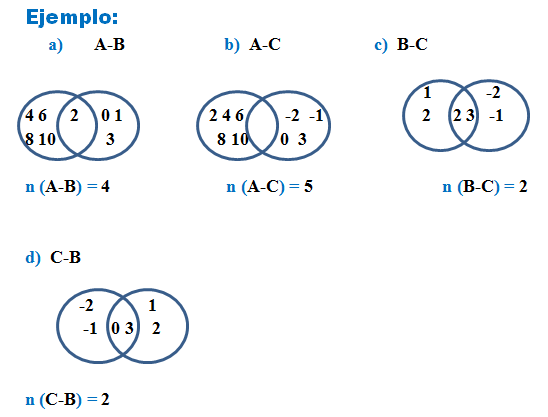

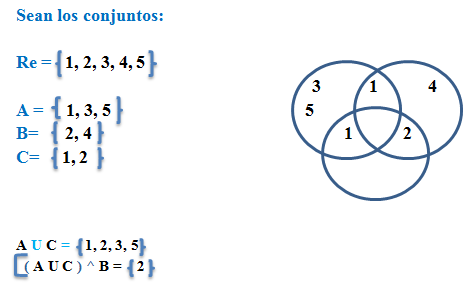


 o { }
o { } A
A